Generative Models for Simulation of Realistic Ocean Currents

This work was part of my masters degree in Robotics and AI at TU Munich, conducted at UC Berkeley.

(Lower-powered) Autonomous systems/robots operating in the oceans can use forecast of the currents to anticipate water flows and take advantage of them. The operational ocean forecasts are based on numerical ocean models with coarse 1/12 degree resolution which inherently fail to model small-scale physical effects and make systematic errors. Hence, to accurately quantify the performance of various ocean robot controllers there is a need to go beyond these forecasts and simulate the ocean currents with their true complexity.

But how can realistic ocean currents be simulated? In this thesis generative methods to model the dense spatio-temporal distribution of forecast current errors, grounded by sparse measurements are proposed. Synthetic errors sampled from this error distribution can then be added to coarse forecasts to produce possible realizations of the true currents which enable realistic simulations.

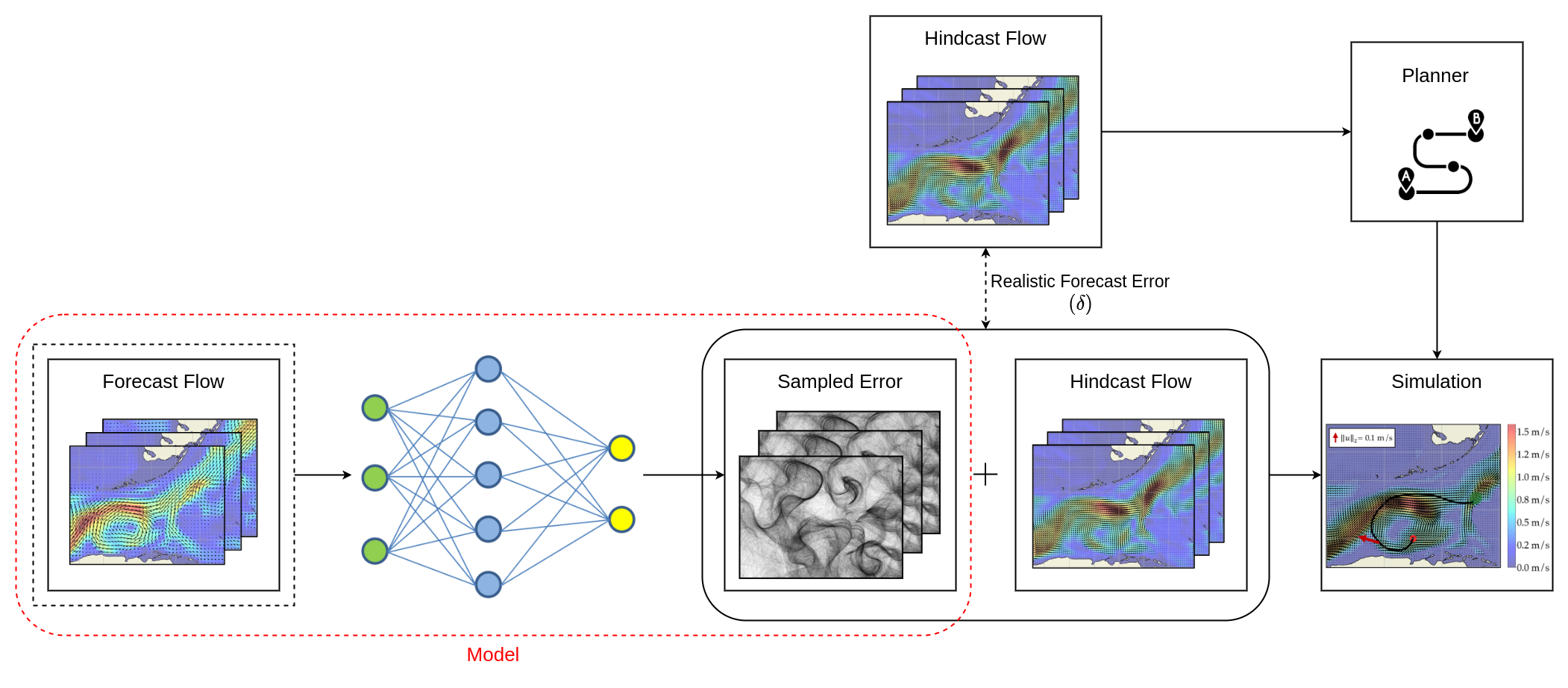
First the empirical forecast error distribution derived from sparse measurements of drifter buoys are analyzed. This analysis and the physical processes governing fluid flows inform the metrics and criteria which are used to measure the performance of the generative methods. Then the Tuned Simplex Noise (TSN) method, which leverages the spatio-temporal correlations of the measured current errors to produce dense spatio-temporally smooth synthetic error fields, is introduced. Experimental analysis suggests that TSN performs well in matching the statistics and characteristics of the empirical forecast errors. However, it was found that in regions where the forecast error is high compared to the forecasted current magnitude, the synthetic errors from TSN can dominate the forecasted currents and change the current structure when added together to produce realistic true currents. This happens because TSN does not have knowledge of the forecast.

Hence, conditional GANs (cGAN) that have knowledge of forecast currents by conditioning on them are investigated. The error samples produced by cGANs were shown to be correlated with the forecast, thus they do not dominate the current structure. While the conditional GAN approach demonstrates promising results, it was found that the diversity of samples collapses when the measurement to original signal ratio is below 15%. In experiments on data from the northern pacific this ration is 0.1%, which renders this approach not suitable for that region.

The thesis makes three core contributions: First the novel problem of learning generative models from extremely sparse ground truths and metrics and criteria for evaluating these models is formalized. Second, two promising methods are developed and their application and evaluation on real ocean current data in the northern pacific is assessed. Third, the conditions under which these approaches work and fail are discussed.

The models developed in this thesis can be applied to similar problems, where only sparse measurements of an environmental variable are available and the original spatio-temporal signal needs to be simulated. If the measurement to original signal ratio is below 15%, TSN a is simple and fast, yet effective solution. If the ratio is larger, one can consider using cGANs which can learn more nuances of the complex spatio-temporal distribution.